Cara menyelsaikan matriks invers ordo 3x3
Suatu matriks dapat dibalik jika dan hanya jika matriks
tersebut adalah matriks persegi (matriks yang berukuran n x n) dan
matriks tersebut non-singular (determinan 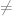 0). Tidak semua matriks memiliki invers. Invers matriks dapat didefinisikan sebagai berikut.
0). Tidak semua matriks memiliki invers. Invers matriks dapat didefinisikan sebagai berikut.
Definisi :
Jika A adalah suatu matriks kuadrat, dan jika kita dapat
mencari matriks B sehingga AB = BA = I, maka A dikatakan dapat dibalik
(invertible) dan B dinamakan invers dari A
Bagaimana cara menghitung invers jika matriksnya memiliki ordo
lebih dari 2? Misal matriks 3×3, 4×4, dan seterusnya. Pada matriks yang
berordo lebih dari dua ini kita akan memanfatkan Eliminasi Gauss Jordan.
Contoh :
Carilah invers matriks 3×3 yaitu A = ![\left [\begin{array}{rrr} 1& 2& 3\\ 2& 5& 3\\ 1& 0& 8 \end{array} \right ] \left [\begin{array}{rrr} 1& 2& 3\\ 2& 5& 3\\ 1& 0& 8 \end{array} \right ]](https://s0.wp.com/latex.php?latex=%5Cleft+%5B%5Cbegin%7Barray%7D%7Brrr%7D+1%26+2%26+3%5C%5C+2%26+5%26+3%5C%5C+1%26+0%26+8+%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
Penyelesaian :
Susun matriks sedemikian sehingga seperti dibawah ini.
Matriks disebelah kiri adalah matriks A dan sebelah kanan adalah matriks identitas. Kemudian lakukan Operasi Baris Elementer
sedemikan sehingga matriks sebelah kiri menjadi matriks identitas dan
matriks identitas (pada sebelah kanan) yang akan menjadi invers matriks
tersebut.
baris kedua : B2 + (-2B1) [artinya baris kedua dijumlahkan dengan -2 kali baris pertama]
baris ketiga : B3 + (-B1) [artinya baris kedua dijumlahkan dengan -1 kali baris pertama]
baris ketiga : B3 + 2B2 [artinya baris ketiga dijumlahkan dengan 2 kali baris kedua]
baris ketiga : B3 x (-1) [artinya baris ketiga dikali dengan -1]
baris kedua : B2 + 3B3 [artinya baris kedua dijumlahkan dengan 3 kali baris ketiga]
baris pertama : B1 + (-3B3) [artinya baris pertama dijumlahkan dengan -3 kali baris ketiga]
baris pertama : B1 + (-2B2) [artinya baris pertama dijumlahkan dengan -2 kali baris kedua]
Karena matriks kiri sudah terbentuk menjadi matriks identitas, maka invers dari matriks A adalah A-1 = ![\left [\begin{matrix} -40& 16& 9\\ 13& -5& -3\\ 5& -2& -1 \end{matrix} \right ] \left [\begin{matrix} -40& 16& 9\\ 13& -5& -3\\ 5& -2& -1 \end{matrix} \right ]](https://s0.wp.com/latex.php?latex=%5Cleft+%5B%5Cbegin%7Bmatrix%7D+-40%26+16%26+9%5C%5C+13%26+-5%26+-3%5C%5C+5%26+-2%26+-1+%5Cend%7Bmatrix%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
Contoh :
Periksa apakah matriks A3×3 memiliki invers? Jika, tentukan inversnya, dengan A = ![\left [\begin{matrix} 3& 1& 5\\ 2& 4& 1\\ -4& 2& -9 \end{matrix} \right ] \left [\begin{matrix} 3& 1& 5\\ 2& 4& 1\\ -4& 2& -9 \end{matrix} \right ]](https://s0.wp.com/latex.php?latex=%5Cleft+%5B%5Cbegin%7Bmatrix%7D+3%26+1%26+5%5C%5C+2%26+4%26+1%5C%5C+-4%26+2%26+-9+%5Cend%7Bmatrix%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0) .
.
Penyelesaian :
baris pertama : B1 x (1/3)
baris kedua : B2 + (-2B1)
baris ketiga : B3 + 4B1
Perhatikan matriks sebebelah kiri pada baris kedua dan ketiga. Karena
baris kedua dan ketiga memiliki entry yang sama, ini mengakibatkan
matriks tersebut memiliki dterminannya nol, sehingga matriks tersebut
tidak memiliki invers.
Sebelum
menyelesaikan soal matriks, perlu diketahui bagaimana cari determinan matriks
terlebih dahulu. Berikut cara penyelesaiannya.
Rumus:
1. Determinan Matriks ordo 2x2
A =  maka
|A| =
maka
|A| =  = ad-bc
= ad-bc
2. Determinan Matriks ordo 3x3
A =  maka
|A| =
maka
|A| = 
Maka |A| = a11a22a33
+ a12a23a31 + a13a21a32
– a31a22a13 – a32a23a11
– a33a21a12
INVERS MATRIKS
1. Matriks
bujur sangkar berordo (2x2), dapat dirumuskan sebagai berikut:
Jika A =  maka
(invers) A-1 =
maka
(invers) A-1 = 

Contoh.
= 

= 

= 
 =
=  (setiap elemen dikalikan 1/2)
(setiap elemen dikalikan 1/2)
Matriks ordo 3x3, untuk mencari invers matriks ordo 3x3, perlu pemahama matriks-matriks berikut:
Matriks Kofaktor
Adjoin
Nilai elemen
rumus invers Matriks ordo 3 x 3
Keterangan :
Matriks Kofaktor adalah
matriks yang unsurnya diganti dengan nilai determinan yang unsurnya tidak
sebaris dan tidak sekolom dengan unsur asal. Untuk tandanya digunakan
tanda positif negatif saling bergantian.
Adjoin
adalah matriks kofaktor yang di Transposkan
( baris jadi kolom , kolom jadi baris )
Oke langsung ke contoh
soal berikut ini :
Carilah Invers matriks
dari A diatas !!
Langkah pertama maka kita harus mencari kofaktor dari A , dengan cara sbb:
Langkah
kedua, Setelah hasil
dari Kofaktor A ditemukan , maka kita mencari ADJOIN nya =
Langkah ketiga , Mencari nilai determinan A :
Langkah terakhir adalah
mencari invers matriks A dengan rumus :
Invers Matriks nxn = 1 /
nilai determinan . Matriks Adjoinnya
jadi matriks invers A adalah =
SIFAT-SIFAT INVERS MATRIKS
Sifat-sifat ini digunakan dalam operasi hitung invers matriks:
AA-1
= A-1 A = 1
(A-1
) = A
(AB)-1
= B-1 A-1
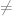 0). Tidak semua matriks memiliki invers. Invers matriks dapat didefinisikan sebagai berikut.
0). Tidak semua matriks memiliki invers. Invers matriks dapat didefinisikan sebagai berikut.![\left [\begin{array}{rrr} 1& 2& 3\\ 2& 5& 3\\ 1& 0& 8 \end{array} \right ] \left [\begin{array}{rrr} 1& 2& 3\\ 2& 5& 3\\ 1& 0& 8 \end{array} \right ]](https://s0.wp.com/latex.php?latex=%5Cleft+%5B%5Cbegin%7Barray%7D%7Brrr%7D+1%26+2%26+3%5C%5C+2%26+5%26+3%5C%5C+1%26+0%26+8+%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
![\left [\begin{matrix} -40& 16& 9\\ 13& -5& -3\\ 5& -2& -1 \end{matrix} \right ] \left [\begin{matrix} -40& 16& 9\\ 13& -5& -3\\ 5& -2& -1 \end{matrix} \right ]](https://s0.wp.com/latex.php?latex=%5Cleft+%5B%5Cbegin%7Bmatrix%7D+-40%26+16%26+9%5C%5C+13%26+-5%26+-3%5C%5C+5%26+-2%26+-1+%5Cend%7Bmatrix%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
![\left [\begin{matrix} 3& 1& 5\\ 2& 4& 1\\ -4& 2& -9 \end{matrix} \right ] \left [\begin{matrix} 3& 1& 5\\ 2& 4& 1\\ -4& 2& -9 \end{matrix} \right ]](https://s0.wp.com/latex.php?latex=%5Cleft+%5B%5Cbegin%7Bmatrix%7D+3%26+1%26+5%5C%5C+2%26+4%26+1%5C%5C+-4%26+2%26+-9+%5Cend%7Bmatrix%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0) .
. maka
|A| =
maka
|A| =  = ad-bc
= ad-bc maka
|A| =
maka
|A| = 
 maka
(invers) A-1 =
maka
(invers) A-1 = 

 maka
A-1 =
maka
A-1 = 






 =
=  (setiap elemen dikalikan 1/2)
(setiap elemen dikalikan 1/2)
Tidak ada komentar:
Posting Komentar